
In Section 3, experimental results using two multiplexed volume holographic gratings in VHIS are measured to characterize volumetric diffraction effects. In addition, we describe the simulation procedure for aperiodic and multiplexed holographic gratings.
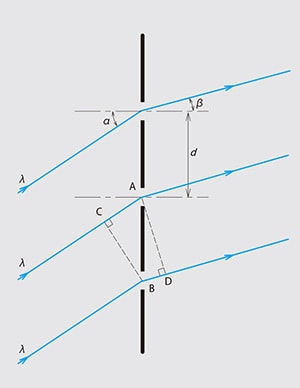
In Section 2, we review the relevant features of approximate and rigorous coupled wave theories used in our model. The simulation results are compared and are found to agree well with experimental measurements of multiplexed volume holographic gratings formed in PQ-PMMA. In addition, our approach can be extended to multiplexed gratings. With ray-tracing implementation, our approach can provide a fast estimation for characterizing volume holographic gratings in imaging systems. The coupled wave approach considers arbitrary polarization of the different fields in the diffraction process with any hologram thickness. RCW with sequential ray-tracing and ACW analysis with non-sequential ray-tracing algorithms will be introduced. In our method, aperiodic and multiplexed gratings will be analyzed by considering locally planar gratings based on Syms’ method incorporating ray-tracing and coupled wave (ACW and RCW) theory. In this paper, we present a comprehensive methodology to model volumetric diffraction effects including depth selectivity and diffraction efficiency of curved gratings in volume holographic imaging systems (VHIS). In case of volume holograms of high-diffractive efficiency, the approximation breaks down because the incident light is strongly depleted. This technique is based on wave optics under assumptions of weak interaction among the incident and diffracted light. In Ref, the Born approximation was used to obtain analytical models for volume holographic gratings. However, it is based on wave optics and not convenient for design process. Syms and Solymar demonstrated treating a grating with localized planar grating sections of variable in orientation across the hologram. Several attempts have been made to analytically evaluate varied k-vector holographic gratings. However, the formation of aperiodic gratings with varied k-vectors is a process more complicated than that of the planar ones. Wissman recently demonstrated to the analysis of planar holographic gratings with a k-sphere formulation to predict volumetric gratings’ diffraction efficiency.
Kogelnik’s two-beam approximate coupled-wave (ACW) analysis and rigorous coupled-wave (RCW) theory have been used extensively to model diffraction effects of uniform gratings formed by two plane waves. Therefore, an accurate methodology to predict the performance of volume holographic gratings is necessary to optimize their design and fabrication with different construction parameters. These include depth selective, hyper-spectral, and fluorescence imaging, and long working distance profilometry.

Volume holographic imaging systems (VHIS) consisting of volume holographic gratings as specialized spatial-spectral filters have recently been successfully applied to microscopic and spectroscopic application.


 0 kommentar(er)
0 kommentar(er)
